Path Planning - A*, D* and more

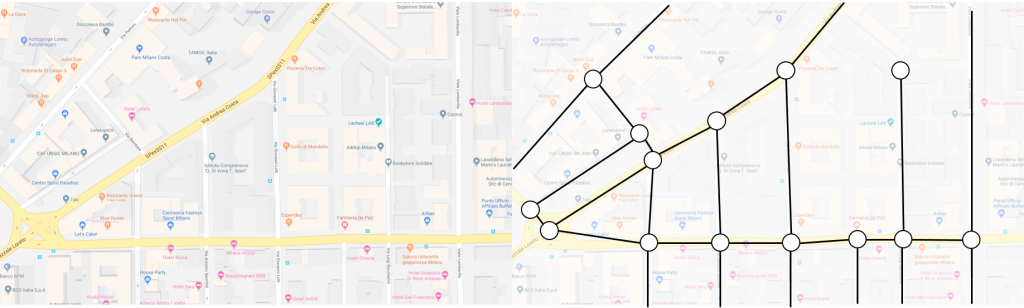
I’ve been on a road trip for the past couple of days, which means I’ve spent a lot of time dealing with Google Maps. As annoying as rerouting every 5 minutes can be, it’s pretty cool that navigation apps are able to dynamically plan paths around traffic and changing road conditions. How do they work, though?

We can represent all our possible paths as a graph where each road is an edge with a weight corresponding to the time it would take to traverse this road. In reality, this weight could encode factors such as distance, traffic, and time of day to give an accurate representation of how much it would cost us to take this path. Each node represents a junction in the roads and is where our planning actually occurs.

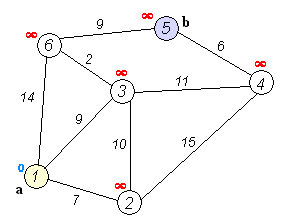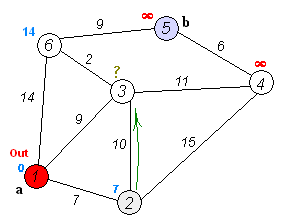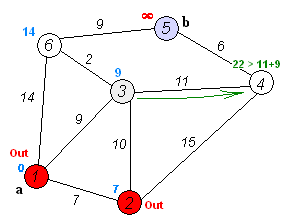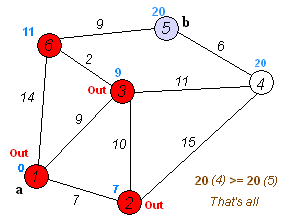
Let’s look at Dijkstra’s algorithm first - essentially, we take all of the nodes that are visible to us from the start node and pick the lowest cost one. Then, we mark this edge as “visited,” and we update the edges that are now visible since we are at a new node. Then, we pick the lowest cost edge from the updated list and keep going until we reach the goal!

Next, let’s look at A*, which uses additional information about our graph to make a more informed estimate of where to go. Before, we would pop the node with the lowest weight to get to, but what if we could also estimate the cost to get to the goal? Given nodes Start, A, and Goal, we want to minimize the cost to get from Start to A as well as the cost to get from A to Goal. However, since we don’t usually know the precise cost to get from A to Goal, we have to use an estimate, or heuristic. Our heuristic is considered “admissible” if it overestimates the cost to get to the goal. More formally, we sort our priority queue for picking nodes by f(n) = g(n) + h(n), where g(n) is the cost to get to node n from the start and h(n) is the heuristic to get from node n to the goal.

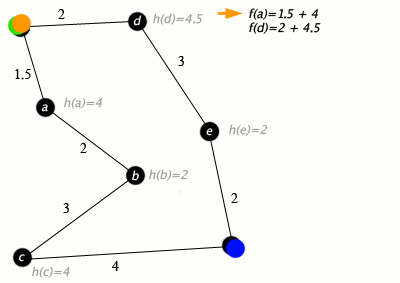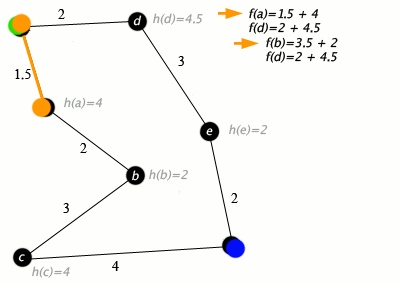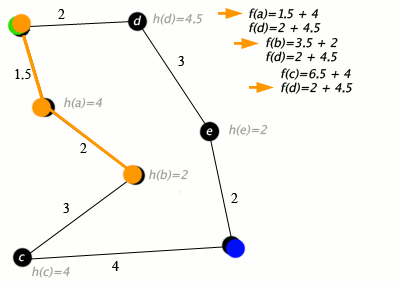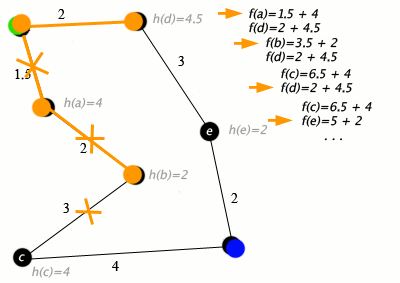
Djikstra’s and A* work for static maps, but what if the environment is constantly changing? We don’t want to recomupute the path at every step - at least not the whole path. First described by Koenig and Likhachev in the paper Incremental A, Lifelong Planning A (LPA*) improves the performance of A* in a dynamically changing environment by taking propagating changes that are seen while traversing a dynamic environment. More specifically, every node n has a predecessor n’ from which it is extended, and the node is considered locally consistent if g(n) equals rhs(n). The value rhs(n) is defined as g(n’)+d(n’,n), where d(n’,n) yields the cost of getting from n’ to n. Basically, a node is inconsistent if the cost to get from the node to the goal is not equal to the cost to get from the node to its parent plus the cost to get from the parent to the goal.

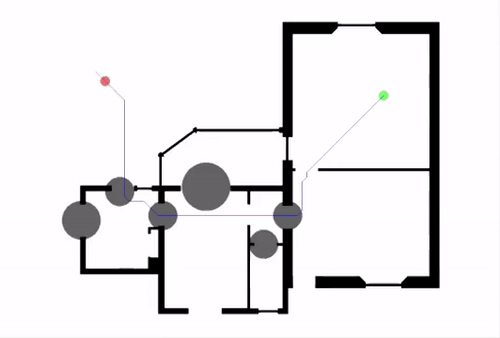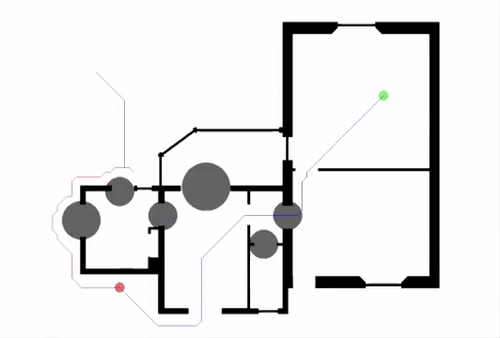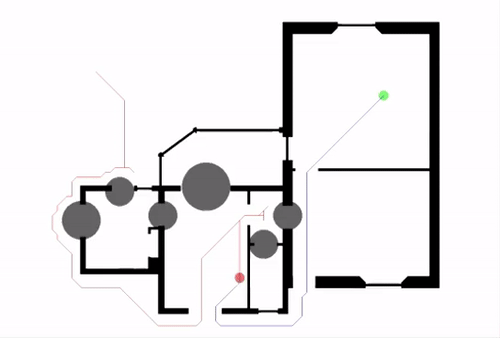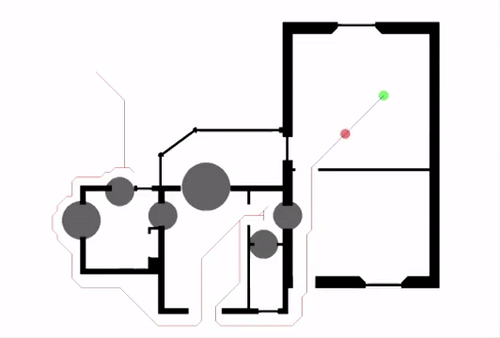
Nodes are added to a priority queue for reevaluation when they are locally inconsistent and keyed by two values: first, min{g(n), rhs(n)} + h(n), and second, min{g(n), rhs(n)}. If rhs(n) is less than g(n) (locally overconsistent, the parent n’ is now more cheaply reachable), g(n) is set to rhs(n), and if rhs(n) is greater than g(n) (locally underconsistent, the node n is more costly to be reached from n’ than previously determined), g(n) is set to infinity. After this, if the node is locally consistent, we pop it from the queue; otherwise, we update its key and add it back to the queue. Since updating the g-value of a node may also affect the rhs-value of the node’s successors, all of the node’s successors are also reevaluated, leading to a cascading effect as new obstacles are discovered. LPA* essentially allows only a few of the nodes to be expanded again every time an obstacle is encountered rather than all the nodes of the A* graph, which is relatively efficient.

I’ve personally worked on improving LPA*, which you can read more about here: https://github.com/ishanchadha01/Field-Aided-RRT

Also, you can check out the Incremental A* paper here: https://ai.dmi.unibas.ch/research/reading_group/koenig-likhachev-nips2002.pdf